给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
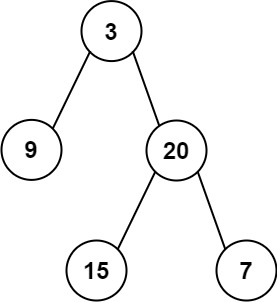
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
- 1 <= inorder.length <= 3000
- postorder.length == inorder.length
- -3000 <= inorder[i], postorder[i] <= 3000
- inorder和postorder都由 不同 的值组成
- postorder中每一个值都在inorder中
- inorder保证是树的中序遍历
- postorder保证是树的后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| /**
* 递归法
* 1、确立当前节点
* 2、确立当前节点的左节点
* 3、确立当前节点的右节点
* 4、返回当前节点
*
* @param inorder 中序数组
* @param postorder 后序数组
* @return 结果树
*/
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (postorder == null || postorder.length == 0) {
return null;
}
TreeNode curNode = new TreeNode(postorder[postorder.length - 1]);
//返回条件,当前是叶子节点
if (postorder.length == 1) {
return curNode;
}
//根据cur,切割inorder 找出切割点
int leftLen = 0;
while (inorder[leftLen] != curNode.val) {
leftLen++;
}
//中序数组的左子集合,请注意上面的写法多加加了一次 Arrays.copyOfRange 这个方法是左闭右开
int[] inleft = Arrays.copyOfRange(inorder, 0, leftLen);
//中序数组的右子集合
int[] inright = Arrays.copyOfRange(inorder, leftLen + 1, inorder.length);
//后序数组的左子集,注意这里必须要使用 中序数组的左子集长度
int[] postleft = Arrays.copyOfRange(postorder, 0, inleft.length);
int[] postright = Arrays.copyOfRange(postorder, inleft.length, postorder.length - 1);
curNode.left = buildTree(inleft, postleft);// 中序数组的左子集合,后序数组的左子集
curNode.right = buildTree(inright, postright);// 中序数组的右子集合,后续数组的右子集
return curNode;
}
|
