按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n皇后问题 研究的是如何将 n个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的n皇后问题 的解决方案。
每一种解法包含一个不同的n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
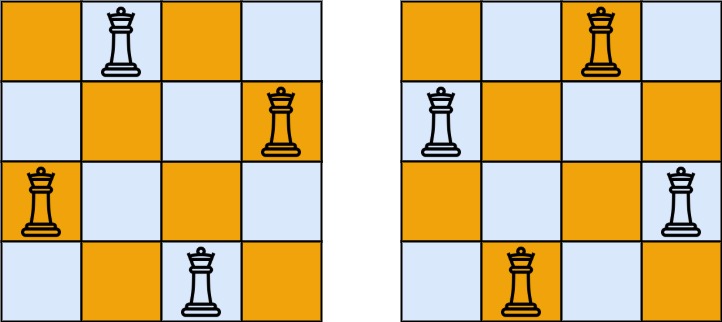
示例 1:
输入:n = 4
输出:[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[[“Q”]]
提示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
/**
* 51. N 皇后
*/
public class LeetCode51 {
/**
* N皇后的问题,从很早开始就有接(tu)触(cao),但是忘记了在哪里看到
* 虽然平时不玩国际象棋,但是规则多多少少都知道一点,就是“皇后”是机动能力最强的兵种,可以横、竖、对角线都能移动,除非该线路上有障碍物
* 然后这道题的变态点就是N*N棋盘,能否放N个皇后,如果可以,列举除所有的摆放方法
* 无他的,假如遇到这种问题,只能尝试下回溯法(穷举),一个一个格子填放皇后,判断是否符合要求,不符合要求,就回滚,滚滚滚。。。
*/
public List<List<String>> solveNQueens(int n) {
char[][] ca = new char[n][n];
for (char[] c : ca) {//只能一行一行的填充
Arrays.fill(c, '.');
}
tracking(n, 0, ca);
return rt;
}
private void tracking(int n, int row, char[][] ca) {
//只有当前遍历的层数到达最底层,才能将数据填写到最终结果
if (row == n) {//数组下标是从0开始的
rt.add(array2List(ca));
return;
}
for (int i = 0; i < n; i++) {
if (isValue(n, row, i, ca)) {
ca[row][i] = 'Q';
tracking(n, row + 1, ca);
ca[row][i] = '.';//这里要注意需要填写“.”,需要审题,哈哈哈
}
}
}
/**
* 结果集的转换
*/
private List<String> array2List(char[][] array) {
List<String> list = new ArrayList<>();
for (char[] c : array) {
list.add(String.copyValueOf(c));
}
return list;
}
/**
* 判断当前位置能否填放皇后
*
* @param n 总行数
* @param row 当前行
* @param col 当前列
* @param ca 已存放二维结果集结果
* @return 判断能否存放
*/
private boolean isValue(int n, int row, int col, char[][] ca) {
//如果当前位置的垂直往上的行已经存在皇后则false
for (int i = 0; i < row; i++) {
if (ca[i][col] == 'Q') {
return false;
}
}
//如果当前位置的左斜上角已经存在皇后,则false
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (ca[i][j] == 'Q') {
return false;
}
}//如果当前位置的右斜上角已经存在皇后,则false,要小心边界
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (ca[i][j] == 'Q') {
return false;
}
}
return true;
}
private List<List<String>> rt = new ArrayList<>();
}
|
