给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
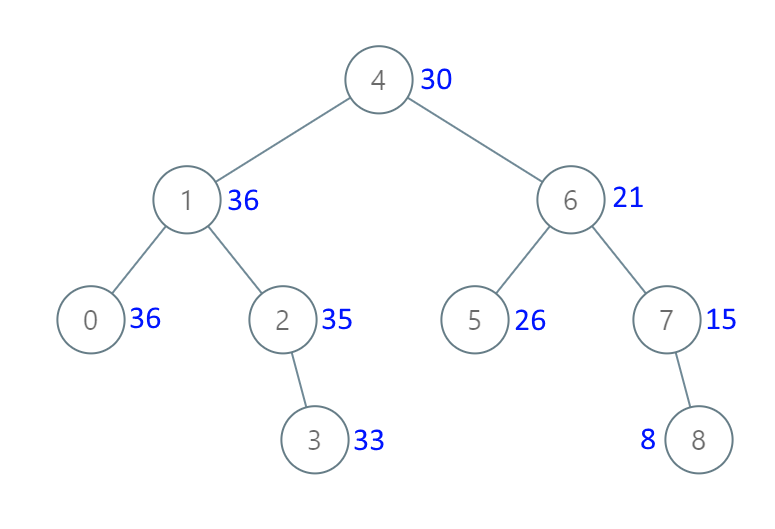 示例 1:
示例 1:
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于 0和 10^4之间。
- 每个节点的值介于 -10^4和10^4之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| /**
* 初始看这道题的描述,只想说Oh my god,说的是啥?
* 一翻评论区,发现很多人有相同的想法
* 其实这道题说的就是转变第一个节点是所有 当前节点+右侧节点之和
* 同理第二个节点新值为 当前节点+右侧节点之和
* 所以通过上述描述,自然也就简单了
* 在遍历节点我们有前、中、后序遍历,这里得要使用中序遍历,不过是反过来的中序,也就是 右中左的顺序
*/
public TreeNode convertBST(TreeNode root) {
if (root == null) {//递归的必要介绍条件
return null;
}
root.right = convertBST(root.right);//右
if (pre != null) {
//上一个节点+本节点之和赋值给当前节点
root.val = pre.val + root.val;
}
//当前节点赋给前置节点
pre = root;
root.left = convertBST(root.left);//左
return root;
}
//前置节点
private TreeNode pre = null;
|
 示例 1:
示例 1: