给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
示例 1:
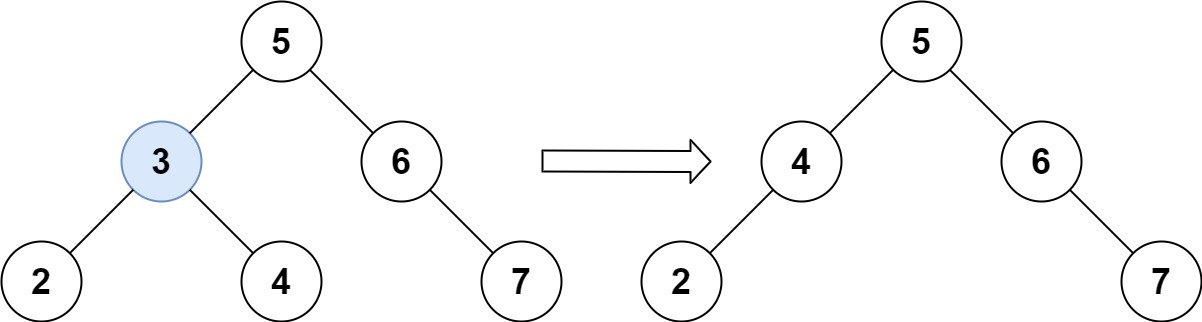
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
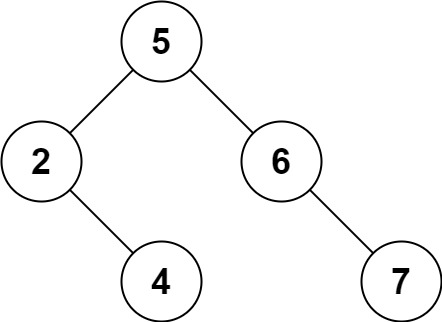
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围[0, 10^4].
- -10^5<= Node.val <= 10^5
- 节点值唯一
- root是合法的二叉搜索树
- -10^5<= key <= 10^5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| /**
* 删除节点会有5种情况需要考虑,我在会代码上注释
* 这个还是中序遍历
*/
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return root;
}
//如果找到节点
if (root.val == key) {
if (root.left == null && root.right == null) {
//左右孩子都是空,返回null(表示当前节点已经删除)
return null;
} else if (root.right == null) {
//右空,左不空 返回当前节点的左节点
return root.left;
} else if (root.left == null) {
//同理
return root.right;
} else {
//左右孩子都不为空,那么就将左孩子挂到 右子树的最左叶子节点上
//那么就需要找到右子树的最左叶子
TreeNode cur = root.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = root.left;
root = root.right;
return root;
}
} else if (key < root.val) {
//小于就左
root.left = deleteNode(root.left, key);
} else {
//大于就右
root.right = deleteNode(root.right, key);
}
return root;
}
|

