给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
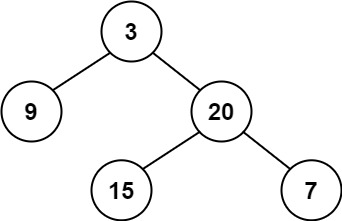
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
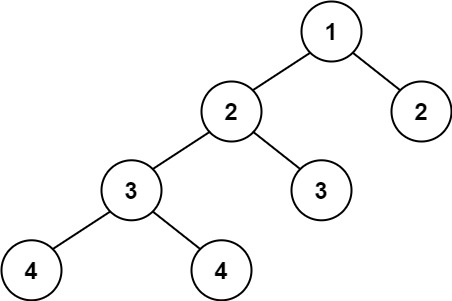
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| /**
* 这道题也可以稍微参考下104
* 一开始接触这道题的时候,觉得,这怎么可能是到easy 题,至少用迭代法,会复杂很多,所以只能先掌握递归
* 1、还是从宏观上考量,分成三个节点,root、left、right,左子树是否平衡,右子树是否平衡,当前树是否评审
* 2、假如我们使用后序遍历,那么上面的问题可以简单的归纳为 当前叶子节点的上级节点是否平衡
* 3、需要一个获取高度的函数
* 4、通过高度差的计算判断是否平衡二叉树
*/
public boolean isBalanced(TreeNode root) {
return depth(root) != -1;
}
/**
* @param node 当前节点
* @return 当前节点最大高度
* 假如不是平衡树,返回-1
*/
public int depth(TreeNode node) {
if (node == null) {
return 0;
}
//后序遍历
int left = depth(node.left);
if (left == -1) {
return -1;
}
int right = depth(node.right);
if (right == -1) {
return -1;
}
//到这步,左右子树都是平衡二叉树
//如果高度差大于1,就不是平衡树,返回-1,否则返回最大的深度+1
return Math.abs(left - right) > 1 ? -1 : Math.max(left, right) + 1;
}
|

